随机相近似

RPA的基本概念在多体物理中扮演着核心的角色，它由Bohm和Pines在1950年代提出[1,2]，目的是描述均匀正电荷背景下运动的均匀电子气相互作用的集体特性。从量子多体微扰理论的角度来看，原始的RPA等效于Ring diagram的无限求和[3], 如图1a。Perdew等人在70年代首先将RPA纳入进DFT框架[4]，使得RPA成为适用于计算真实材料的基态能量的第一原理方法。在DFT框架下，根据公认的交换关联泛函的分类方案(图1b)，RPA可被视为E_xc泛函的五阶近似。然而，由于RPA巨大的计算量，首次在具体材料体系上应用直到2001年由Furche实现[5]。随后，RPA 被应用到一系列体系中，包括原子体系[6]、分子体系[7]、固体[8]、表面[9]、缺陷[10]和层状材料[11]等。大量的证据表明，RPA可以以相对不是很高的计算成本极大地提升预测材料基态性质的准确性。这里，我们推荐Ren等人的综述[12,13]，Pines近期的综述[14]以及Furche最近的综述[15]。

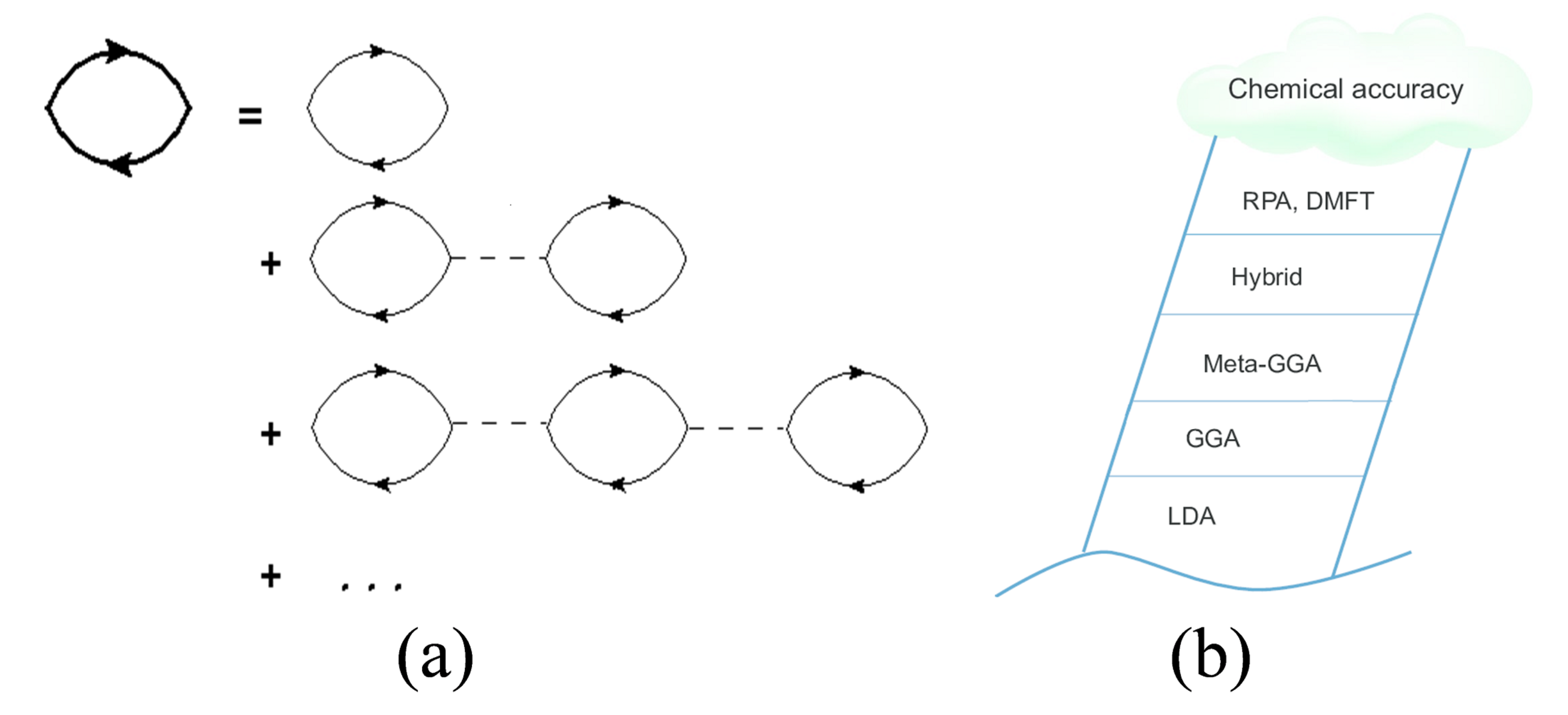
图1. (a) 对Ring diagram进行求和从而实现RPA。上方的粗线表示相互作用的格林函数，非粗线表示无相互作用的格林函数，而虚线表示两体相互作用。(b) DFT Jacobs 阶梯图。

RPA可以从多个理论框架下获得，包括Coupled cluster theory [16], Green-function based many-body perturbation theory [17], Time-dependent DFT (TDDFT) [5] 以及Adiabatic connection fluctuation-dissipation theorem (ACFDT)[4,18]。这里我们暂时只介绍ACFDT-RPA过程。

1 ACFDT-RPA

前面我们在介绍DFT部分，给出了adiabatic connection (AC)图像下的DFT。

在KS-DFT下有：

$$E\left[n\right]=T_\mathrm{s}\left[\psi_n\right]+E_{\mathrm{ext}}\left[n\right]+E_\mathrm{H}\left[n\right]+E_{\mathrm{xc}}\left[n\right]$$

其中E_ext和E_H为n(r)的显函数，T_s为无相互作用体系单粒子轨道表示，而只有E_XC是未知的。通过AC可以获得E_XC的精确的表达式，用密度-密度关联函数表示为：

$$ E_{\mathrm{xc}}[n]=\int_{0}^{1} d \lambda \frac{1}{2} \iint d \boldsymbol{r} d \boldsymbol{r}^{\prime} \frac{\left\langle\Psi\left|\delta \hat{n}(\boldsymbol{r}) \delta \hat{n}\left(\boldsymbol{r}^{\prime}\right)\right| \Psi_{\lambda}\right\rangle- n(\boldsymbol{r}) \delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right)}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|} $$

在构建LDA，GGA和meta-GGA等泛函时，仅包含了局域或半局域的量，例如电子密度、密度梯度和动能密度等，而杂化泛函中包含了非局域量-约化密度矩阵。如果要比这些近似走得更远，则需要包含真实物理系统中的更多信息。出与这一目的，有必要加入零温度波动耗散定理[4]，该理论将密度与密度之间的关联(涨落)与系统的密度响应函数的虚部(耗散)相联系，即：

$$ \left\langle\Psi_{\lambda}\left|\delta \hat{n}(\boldsymbol{r}) \delta \hat{n}\left(\boldsymbol{r}^{\prime}\right)\right| \Psi_{\lambda}\right\rangle=-\frac{1}{2 \pi} \int_{-\infty}^{\infty} d \omega \operatorname{Im} \chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, \omega\right) $$

其中密度响应函数 $$\chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, \omega\right)=\delta n_{\lambda}(\boldsymbol{r}, \omega) / \delta v^{ext}\left(\boldsymbol{r}^{\prime}, \omega\right)$$ 描述了在空间在r处的部分相互作用体系的密度由于在r'局域势的变化所产生的变化。由此，我们获得：

$$ E_{\mathrm{xc}}=\frac{1}{2} \int_{0}^{1} d \lambda \iint d \boldsymbol{r} d \boldsymbol{r}^{\prime} \frac{1}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|}\left(-\frac{1}{2 \pi} \int_{-\infty}^{\infty} d \omega \operatorname{lm} \chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, \omega\right)-\delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right) n(\boldsymbol{r})\right) $$ $$ = \frac{1}{2} \int_{0}^{1} d \lambda \iint d \boldsymbol{r} d \boldsymbol{r}^{\prime} \frac{1}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|}\left(-\frac{1}{\pi} \int_{0}^{\infty} d \omega \chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)-\delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right) n(\boldsymbol{r})\right) $$

上述频率积分可以在虚轴上执行，源于 \(\chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, \omega\right)\) 的解析结构及其在虚轴上为实数的特点，因此可以可观地简化计算复杂度。至此，ACFDT将求解E_XC的问题转换成了计算沿AC路径连续的一组虚拟系统的响应函数的问题，而这一步由于严格的\(\chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, \omega\right)\) 也是未知的，所以仍然需要近似。根据线性响应TDDFT，λ>0的相互作用响应函数χ^λ可以通过Dyson-like方程与无相互作用响应函数χ⁰相联系：

$$ \chi^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)=\chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)+\int d \boldsymbol{r}_{1} d \boldsymbol{r}_{2} \chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}_{1}, i \omega\right)\left[\frac{\lambda}{\left|\boldsymbol{r}_{1}-\boldsymbol{r}_{2}\right|}+f_{\mathrm{xc}}^{\lambda}\left(\boldsymbol{r}_{1}, \boldsymbol{r}_{2}, i \omega\right)\right] \chi^{\lambda}\left(\boldsymbol{r}_{2}, \boldsymbol{r}^{\prime}, \omega\right) $$

其中，

$$ f_{xc}\left(\boldsymbol{r}_{1}, \boldsymbol{r}_{2}, i \omega\right)=\frac{\delta v_{\mathrm{xc}}\left(\boldsymbol{r}_{1}\right)}{\delta n\left(\boldsymbol{r}_{2}, \omega\right)}=\frac{\delta^{2} E_{\mathrm{xc}}[n]}{\delta n\left(\boldsymbol{r}_{1}\right) \delta n\left(\boldsymbol{r}_{2}, \omega\right)} $$

被称为核函数，由交换关联势函数相对于与频率相关的密度的导数给出。显然，核函数是一个求解非常复杂的物理量，目前仍在进行大量的工作以寻找关于它更好的近似[19]。在这种情况下，随机相近似等于简单地忽略了核函数，并将由此产生的相互作用响应函数称为RPA响应函数：

$$ \chi_{\mathrm{RPA}}^{\lambda}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)=\chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)+\int d \boldsymbol{r}_{1} d \boldsymbol{r}_{2} \chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}_{1}, i \omega\right) \frac{\lambda}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|} \chi_{\mathrm{RPA}}^{\lambda}\left(\boldsymbol{r}_{2}, \boldsymbol{r}^{\prime}, \omega\right) $$

在物理上，RPA在这里对应于线性化的与时间相关的Hartree近似，通过该近似，可以忽略由于外部扰动引起的交换相关电位的变化。而独立粒子响应函数\(\chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)\)可以由单粒子KS轨道，轨道能量及占据数所给出：

$$ \chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)=\sum_{m n} \frac{\left(f_{m}-f_{n}\right) \psi_{m}^{*}(\boldsymbol{r}) \psi_{n}(\boldsymbol{r}) \psi_{n}^{*}\left(\boldsymbol{r}^{\prime}\right) \psi_{m}\left(\boldsymbol{r}^{\prime}\right)}{\varepsilon_{m}-\varepsilon_{n}-i \omega} $$

结合上式和E_XC沿着AC路径积分响应函数式，可进一步分解RPA E_XC为：

$$ E_{\mathrm{xc}}^{\mathrm{RPA}}=E_{\mathrm{x}}^{\mathrm{EX}}+E_{\mathrm{c}}^{\mathrm{RPA}} $$

其中，

$$ \begin{aligned} E_{\mathrm{x}}^{\mathrm{EX}}=\frac{1}{2} \iint d r d r^{\prime} & \frac{1}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|}\left(-\frac{1}{\pi} \int_{0}^{\infty} d \omega \chi^{0}\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}, i \omega\right)-\delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right) n(\boldsymbol{r})\right) \\ &=-\sum_{m n} f_{m} f_{n} \iint d \boldsymbol{r} d \boldsymbol{r}^{\prime} \frac{\psi_{m}^{*}(\boldsymbol{r}) \psi_{n}(\boldsymbol{r}) \psi_{m}^{*}\left(\boldsymbol{r}^{\prime}\right) \psi_{n}\left(\boldsymbol{r}^{\prime}\right)}{\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|} \end{aligned} $$

该式即KS-DFT中的exact-exchange energy，也等于HF交换能(但此处使用了KS轨道，并将其扩展到允许分数占据数)。

其中\(v\left(\boldsymbol{r}, \boldsymbol{r}^{\prime}\right)=1 /\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|\) 至此，ACFDT框架下RPA过程下的E_XC就描述完了。在实际计算中，体系的总能量将分成两部分分别进行计算，即：

$$ E_{RPA}=E_{EXX}+E_{C} $$

其中等于用KS轨道演化的HF能，它包含动能项，背景离子势能、Hartree能以及交换能，而关联能则由上述RPA给出。这样处理下，具备三个有吸引力的特征：

• Exact-exchange能恰好消除了Hartree能量中的self-interaction误差。
• RPA关联能是完全非局域的，它自动地并且无缝地包含长van der Waals (vdW)相互作用。
• RPA包含了动力学屏蔽效应，即它考虑了一系列“ring”图到无穷阶的求和，使得它可以处理小带隙或者金属体系(这些体系有限阶的多体微扰理论无法处理)。

 

参考文献：

[1]  D. Bohm and D. Pines, Physical Review 82, 625 (1951).

[2]  D. Bohm and D. Pines, Physical Review 92, 609 (1953).

[3]  J. Hubbard, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 240, 539 (1957).

[4]  D. C. Langreth and J. P. Perdew, Solid State Communications 17, 1425 (1975).

[5]  F. Furche, Physical Review B 64, 195120 (2001).

[6]  H. Jiang and E. Engel, The Journal of chemical physics 127, 184108 (2007).

[7]  M. Fuchs and X. Gonze, Physical Review B 65, 235109 (2002).

[8]  J. Harl and G. Kresse, Physical review letters 103, 056401 (2009).

[9]  X. Ren, P. Rinke, and M. Scheffler, Physical Review B 80, 045402 (2009).

[10]  F. Bruneval, Physical review letters 108, 256403 (2012).

[11]  S. Lebègue, J. Harl, T. Gould, J. Ángyán, G. Kresse, and J. Dobson, Physical review letters 105, 196401 (2010).

[12]  X. Ren.

[13]  X. Ren, P. Rinke, C. Joas, and M. Scheffler, Journal of Materials Science 47, 7447 (2012).

[14]  D. Pines, Reports on Progress in Physics 79, 092501 (2016).

[15]  G. P. Chen, V. K. Voora, M. M. Agee, S. G. Balasubramani, and F. Furche, Annual review of physical chemistry 68, 421 (2017).

[16]  R. J. Bartlett and M. Musiał, Reviews of Modern Physics 79, 291 (2007).

[17]  B. Ramberger, T. Schäfer, and G. Kresse, Physical review letters 118, 106403 (2017).

[18]  J. Harl and G. Kresse, Physical Review B 77, 045136 (2008).

[19]  A. Görling, Physical Review B 99, 235120 (2019).